Intro to Machine Learning and AI based on high school knowledge
(This article originally appeared at KDNuggets.com here. For more, visit https://www.kdnuggets.com/)
Machine learning information is becoming pervasive in the media as well as a core skill in new, important job sectors. Getting started in the field can require learning complex concepts, and this article outlines an approach on how to begin learning about these exciting topics based on high school knowledge.
Introduction
Today, Artificial Intelligence (AI) everywhere.
However, it is a complex topic to both teach and learn.
In this article, I outline an approach where you could learn about Artificial Intelligence, Machine Learning(ML), and Deep Learning(DL) based on high school knowledge alone. The later part of the article is based on simple high school math – which should be familiar at a GCSE level (to age 15 years). Even if the math is not familiar to you, you can still learn about machine learning and artificial intelligence from the first part of the article.
Background
Any talk of AI often leads to ‘Terminator’ type discussions (Are robots going to take over humanity?). While the media gets excited about AI, the reality is more mundane. So, before we proceed, let's consider some definitions that we will adopt in this article.
- Artificial intelligence: refers to machines that can reason with some degree of autonomy
- General Artificial Intelligence: relates to machines that have almost complete autonomy. General artificial intelligence is indeed the stuff of science fiction (and hence not a focus of this article)
- Narrow Artificial Intelligence: refers to machines or systems that can learn a task in a specific context – for example – a robotic arm that learns how to pick and sort items on its own (without explicit training).
- Machine Learning: Has a formal definition. Tom Mitchell defines Machine Learning as: “The field of machine learning is concerned with the question of how to construct computer programs that automatically improve with experience.” This definition is expressed as: “A computer program is said to learn from experience (E) with respect to some class of tasks (T), and performance measure (P), if its performance at tasks in T, as measured by P, improves with experience (E).”. Machine Learning is used in a range of applications such as Spam Detection, Credit Card Fraud Detection, Customer Segmentation etc
- Deep Learning: We define Deep Learning as a “machine learning application with automatic feature detection.” We explain this definition in more detail below.
What is Learning?
Let’s start with the question: “What is learning? (in context of machine learning)
In Mitchell’s definition, we interpret the word ‘Learning’ as acquiring the ability to perform the task. For example, if we want a system to identify an object, then the ability to identify an object is the task. To achieve this ability, we could take two opposite approaches:
- We could either explicitly write rules to identify specific objects OR
- We could program the system such that it learns (through the process of training) the ability to identify an object.
The former (rule-based approach) is not practically feasible because we would have to manually write down rules for all possible scenarios. So, the other extreme is more viable. Instead of manually creating rules, we could find the rules from the data itself and then apply the rules to an unseen problem. This idea of learning from a training dataset is the foundation of most machine learning approaches (supervised learning). The process of training involves presenting the system with a set of examples which represent a collection of features of interest. From these examples, the system creates a model – which in turn is used to identify an unseen object. A simplified definition of a model in this context is an algorithm (ex: classification algorithm) trained on a dataset.
Consider the example of predicting house prices. House prices can be influenced by many factors (features) such as the number of bedrooms, proximity to schools, proximity to public transport etc. Predicting the house price based on the features is the outcome. These features are inputs to the supervised learning model, which can predict the price of the house (outcome variable). Types of Problems addressed by machine learning include:
- Classification: Data is assigned to a class – for example spam/no-spam or fraud/no-fraud etc.
- Regression: A value of data is predicted – for example predicting stock prices, house prices, etc.
Finally, how do we know if the system can perform a given task? To test the performance of a model, we must evaluate its output using a quantitative measure specific to the task. For a classification task, the performance of the model could be measured by the accuracy of the classification.
Deep learning
So, how does this relate to Artificial Intelligence and Deep Learning? Remember we characterised Deep learning as ‘Automatic feature detection.' Let us reconsider the example of predicting house prices. To determine the features of this algorithm (ex: number of bedrooms, proximity to good schools, etc.), you need knowledge of the application (domain knowledge). For complex applications – ex in healthcare, genomics etc. domain knowledge can be hard and expensive to acquire. Also, applications that use image, video, sequence, or audio data use hierarchical features. It is impractical for humans to detect these features.
What if we could understand the structure and features of the data (i.e., follow the underlying representation of the data without human intervention?).
This ability is achieved by a set of techniques in machine learning called representation learning. Representation learning is a set of methods that allows a machine to be fed with raw data and to automatically discover the representations needed for algorithms like classification.
Deep-learning methods can be classed as representation-learning methods with multiple levels of representation. These layers start with the raw input, and each layer transforms the data into a higher-level representation – which acts as an input for the subsequent layer. For example, the lowest layer may detect pixels; the next higher layer may detect edges of an image from the pixels; the next layer may detect contours based on the edges, etc. Hence, each layer in the neural network builds on top of the representation from the previous layer. Through many such simple transformations, the machine can learn complicated and hierarchical ideas. The higher-level representations of the neural network model can distinguish between minor variants of a concept, i.e., concepts that are similar but not the same. For example, the network can distinguish between wolves and ‘dogs which look like wolves’ (Huskies, Samoyeds and German shepherds). The same technique can be applied to real problems like tumour detection and other data types – for example – face detection or genomic data.
More generically, Deep Learning techniques are used to work with problems that are not finite-domain. For instance, chess is a finite-domain problem because there are only 64 squares in chess and each piece has a defined action. In contrast, recognising an image of a dog from a picture is easy for a child. But a computer cannot easily recognise pictures of dogs from an image of a dog. Identifying pictures of dogs is not a finite-domain problem since there are many types of dogs in many different configurations in images (ex: with a collar, with their tail cropped etc.)
And to wrap up this idea, artificial intelligence is based mainly on deep learning techniques.
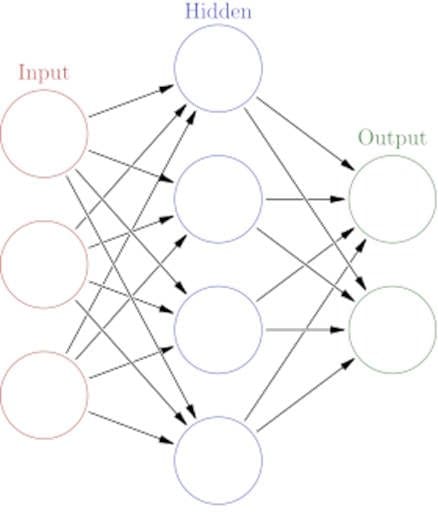
Modelling as function estimation
We could now approach the problem based on basic math.
The process of modelling, which we introduced in the previous section, involves finding a function that represents the data (for example, a function to predict house prices). The function can be expressed as an equation and is used to make predictions on unknown data. The process of fitting a model involves making the algorithm learn the relationship between predictors (features) and outcomes. Once the algorithm determines a functional relationship between the features and the outcome variables, it can predict the values of the outcome variable for unseen features. Hence, the best fitting algorithms have parameters that best depict the problem at hand and can also make predictions on unseen data points. The power of the model, of course, lies in making predictions on unseen data.
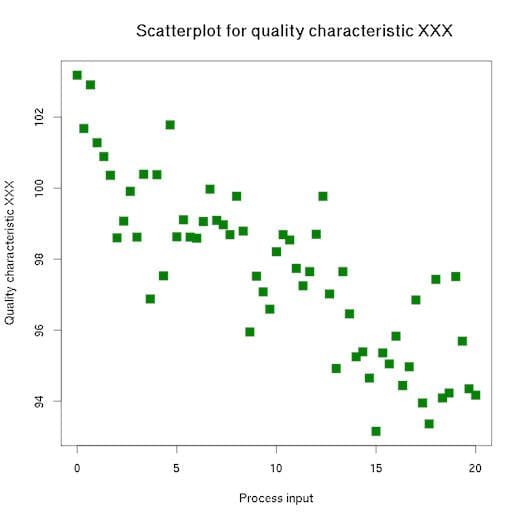
Modelling is an iterative process. It initially involves finding the trends and relationships between variables using a mechanism like a scatter plot. Some relationships are predictable; for example, age and experience are correlated.
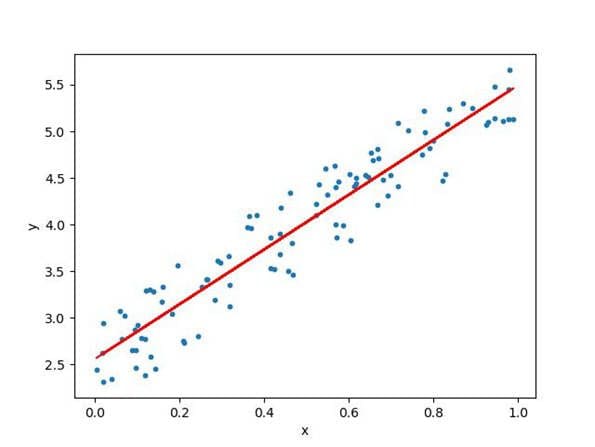
Linear Regression
In the simplest case, that function is linear as represented by a linear relationship
What is a Linear Relationship?
A linear relationship means that you can represent the relationship between two sets of variables with a straight line. A linear relationship can represent many phenomena. For example, the force involved in stretching a rubber band is a linear relationship because the greater the force results in proportionally more stretching of the rubber band. We can represent this relationship in the form of a linear equation in the form:

where “m” is the slope of the line, “x” is any point (an input or x-value) on the line, and “c” is where the line crosses the y-axis. In linear relationships, any given change in an independent variable produces a corresponding change in the dependent variable. Linear regression is used in predicting many problems like sales forecasting and analysing customer behaviour.
The relationship can be represented as below:
Why start with Linear Regression?
Because it is an idea familiar to many even at high school levels, and it also allows us to extend our thinking to more complex ideas. The process of fitting the model aims to find the optimal values of the parameters m and c. We identify a line that best fits the existing data points. Once we've fitted the model, we can use it to predict outcomes (y-axis) based on inputs (x-axis). Training of the model involves finding the parameters so that the model best fits the data. The line for which the total error between the predicted values and the observed values is minimum is called the best fit line or the regression line.
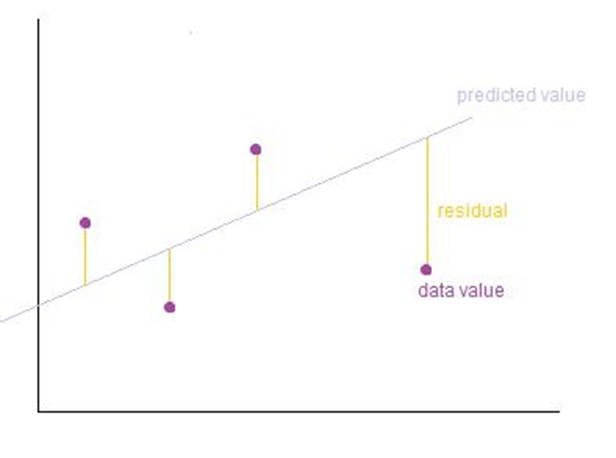
In Ordinary Least Squares (OLS) Linear Regression as described above, our goal is to find the line (or hyperplane) that minimises the vertical offsets. Or, in other words, we define the best-fitting line as the line that minimises the sum of squared errors (SSE).
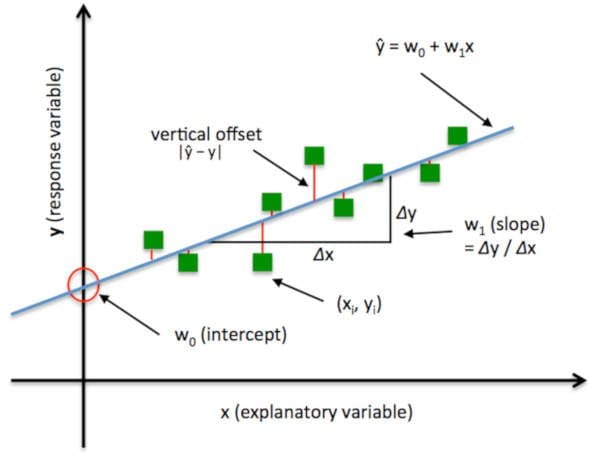
Figure: Ordinary Least Square Regression. Image source.
In this case, the total error to be minimised is

Figure: sum of square errors.
The same idea can be expanded to multiple features. In fact, for the house prices example, we are already using multiple features (x values) to predict an outcome (y value), i.e. the house price. So, instead of y = mx +c, the equation becomes of the form
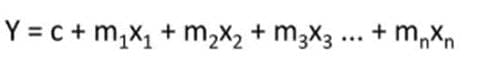
So, the basic GCSE level maths can be used to understand the fundamentals of building and training models.
Conclusion
In this article, we saw how you could get started with machine learning and deep learning using basic high school knowledge. The article is based on a forthcoming book, and we plan to share free copies with a limited number of UK teachers. I am the course director for the Artificial intelligence: Cloud and Edge implementations course at the University of Oxford, and if you are a teacher and interested in these ideas, please connect with me on LinkedIn referring to this article. The views expressed in this article are his own and do not belong to any organisation I am associated with.
Stay in the loop.
Subscribe to our newsletter for a weekly update on the latest podcast, news, events, and jobs postings.



